개발여행의 블로그
트리와 이진트리(Tree and Binary Tree) 본문
트리(Tree)란?
그래프의 일종으로 계층적인 구조를 표현하는 것.
트리(Tree) 예시
· 조직도 ( 회사 등에서 흔히 볼 수 있는 조직도 )
· 디렉토리와 서브디렉토리 구조 ( 컴퓨터에 저장된 폴더의 구조 )
· 가계도
트리(Tree)는 노드(node)들과 노드들을 연결하는 링크(link)들로 구성돼있다.
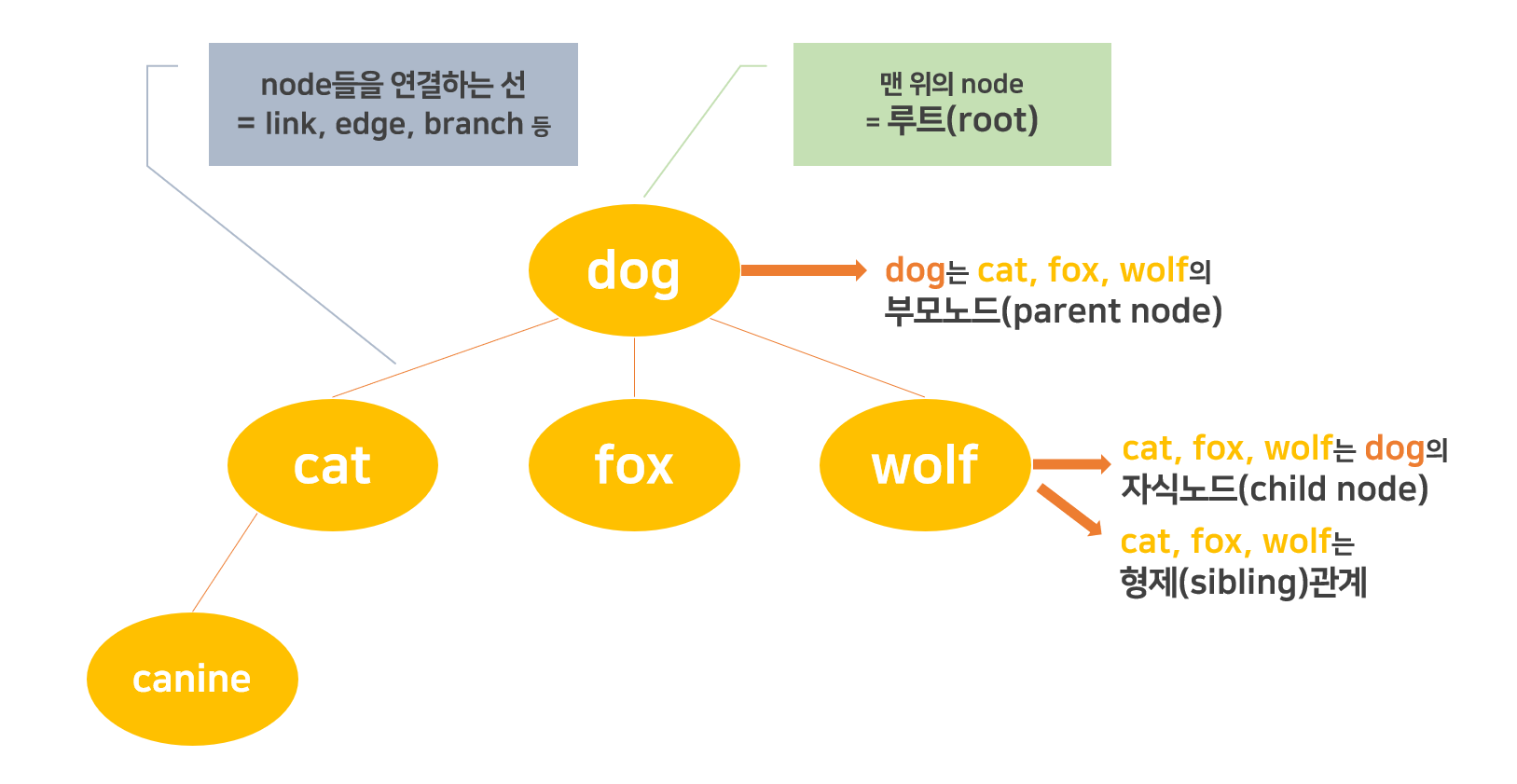
루트(root)노드란?
트리에서 최상위 노드를 루트 노드(root node 뿌리 노드)라고 한다. 위의 그림에서는 dog가 루트 노드이다.
▶ 트리에서 부모-자식 관계
dog는 cat, fox, wolf의 부모 노드(parent node)이고, cat, fox, wolf는 dog의 자식노드(child node)이다.
따라서 root node를 제외한 트리의 모든 node들은 유일한 부모 노드를 가진다.
▶ 트리에서 형제관계
부모가 도일한 노드들을 형제(sibling) 관계라고 부른다. 위 그림에서는 cat, fox, wolf가 형제관계이다.
▶ 리프(leaf)노드란?
자식이 없는 노드들을 리프노드라고 부른다. 위 그림에서는 fox, wolf, canine가 리프노드이다.
▶ 내부(internal)노드란?
리프노드가 아닌 노드들을 내부노드라고 부른다.
▶ 트리에서 조상-자손 관계
부모-자식 관계를 확장한 것이 조상-자손(ancestor-descendant) 관계이다. 위 그림에서 dog는 canine의 조상노드이고, canine은 cat의 자손노드이다.
▶ 부트리=서브트리(subtree)란?
트리에서 어떤 한 노드와 그 노드의 자손들로 이루어진 트리를 부트리(subtree)라고 부른다.

트리에서 레벨은 아래의 그림과 같이 쓰인다. 또한, 여기서 트리의 높이(height)는 서로 다른 레벨의 개수를 의미하는데, 아래 그림의 트리의 높이는 3이다.

▶ 트리의 기본적인 성질
≫ 노드(node)가 N개인 트리는 항상 N-1개의 링크(link)를 가진다.
≫ 루트에서 어떤 노드로 가는 경로가 유일하다. 또한 임의의 두 노드 간의 경로도 유일하다.
(같은 노드를 두 번 이상 방문하지 않는다는 전제하)
이진 트리 (binary tree)
≫ 이진 트리에서 각 노드는 최대 2개의 자식을 가진다.
≫ 각각의 자식 노드는 자신이 부모의 왼쪽 자식인지 오른쪽 자식인지가 지정된다. (자식이 한 명인 경우에도)

▶ 이진트리 응용 예
이진 트리 응용의 예 중에서 하나를 소개하자면 다음과 같은 수식을 표현한 그래프이다.

( x + y ) * ( ( a + b ) / c ) 의 연산을 트리로 표현하면 위의 그림과 같은 것이 된다.
또 다른 이진 트리 응용의 예는 'Huffman code'이다.

Huffman code란 어떤 데이터를 압축하거나 인코딩하는 가장 기본적인 알고리즘 중 하나이다.
예를 들어 어떤 텍스트 파일이 있고, 그 파일을 구성하는 문자는 a-z까지의 알파벳으로 구성되어 있다고 가정해보자. 이 파일에 담긴 알파벳을 적절하게 인코딩하여 최종적으로 그 파일의 길이 최소가 되도록 하는 파일 압축과 관련된 알고리즘 중 하나가 Huffman code이다.
Huffman code에서는 각각 알파벳에 부여된 이진 코드들을 위 그림과 같이 하나의 트리의 형태로 표현할 수 있다.
예를 들어 a는 1 0 1 0으로 인코딩 된다는 의미이다. 마찬가지로 b는 1 0 0 0 0 0로, e는 0 1 0으로 인코딩 되는 것을 의미한다.

▶ Full and Complete Binary Trees
Full Binary Tree란?
모든 레벨에서 노드들이 채워져 있는 트리.

≫ 높이가 h인 full binary tree는 항상 2^h-1개의 노드를 가진다.
≫ 노드가 N개인 full 이진트리의 높이는 O(logN)이다.
노드가 N개인 이진트리의 높이는 최악의 경우 N이 될 수도 있다.
Complete Binary Tree란?
맨 마지막 레벨을 제외한 모든 레벨의 노드들이 채워져 있는 트리.
맨 마지막 레벨 몇 개의 노드가 없을 수 있는데, 오른쪽에서 부터 연속된 노드만 빈자리가 될 수 있다.

≫ 노드가 N개인 full 이진트리의 높이는 O(logN)이다.
노드가 N개인 이진트리의 높이는 최악의 경우 N이 될수도 있다.
▶ 이진트리의 표현

일반적인 이진트리가 된다면 (full 이진트리나 complete 이진트리와 같이 특별한 경우가 아니라면),
규칙성이 성립하지 않기 때문에 이진트리를 표현할 때 연결구조를 이용해서 표현할 수밖에 없다.
각각의 노드가 자기 다음의 노드 주소를 가지고 있는 연결구조이다.
예를 들어 아래의 그림 왼쪽 상단의 트리를 연결 구조로 나타내면 다음과 같다.

위 내용은 '영리한 프로그래밍을 위한 알고리즘 강좌'를 공부하면서 정리한 것입니다.
'개발 > Algorithm' 카테고리의 다른 글
| [알고리즘 javaScript] 숫자 추출 (0) | 2021.11.24 |
|---|---|
| [알고리즘 javaScript] palindrome 팰린드롬:회문 문자열 (0) | 2021.11.24 |
| [유클리드 호제법] Euclidean algorithm (0) | 2021.09.09 |
| [leetcode] 859. Buddy Strings solution(문제 풀이) (0) | 2021.08.21 |
| [leetcode] 7. Reverse Integer 문제 풀이 (0) | 2021.08.15 |

