[leetcode]1557. Minimum Number of Vertices to Reach All Nodes
1557. Minimum Number of Vertices to Reach All Nodes
Minimum Number of Vertices to Reach All Nodes - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
[ 문제 풀이 ]
그래프의 모든 노드에 도달할 수 있는 가장 작은 vertices 집합을 찾는 문제였다. 문제를 한참동안 분석해보아도 파악이 되지 않아 고민하는데에서 시간이 많이 초과되었다. 노드의 개수(n)와 from에서 to 방향을 나타내는 배열 (edges)가 주어질 때, 모든 노드에 도달할 수 있는 가장 작은 정점의 집합을 리턴해야한다.
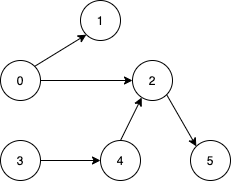
input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
output: [0, 3]
단일 정점에서 모든 노드에 도달하는 것은 불가능한 예시이다. 0에서 [0, 1, 2, 5]에 도달할 수 있고, 3에서 [3, 4, 2, 5]에 도달할 수 있다. 따라서 [0, 3]이 리턴되어야 한다. edges의 방향(from -> to)를 놓쳐서 고민하는 시간이 늘어났는데, 생각해보니 어떤 노드로부터 연결되어 있으면 도달할 수 있기 때문에 length 6의 배열을 하나 선언해두고, to에 해당하는 노드의 인덱스에 count를 계속 더해주었다.
edges에서 [0, 1] 즉, 1은 0에서부터 도달할 수 있기 때문에 [0, 1, 0, 0, 0, 0]으로 인덱스 1의 원소를 1로 변경, [0, 2] 또한 0에서부터 도달할 수 있기 때문에 [0, 1, 1, 0, 0, 0]으로 업데이트 한다. [2, 5]일 때 [0, 1, 1, 0, 0, 1], [3, 4]일 때 [0, 1, 1, 0, 1, 1] 마지막 [4, 2]일 때 [0, 1, 2, 0, 1, 1]이 되어서 도달할 수 없는(원소가 0인) 노드 인덱스 0과 3이 최소의 정점이 되는 것이다.
[ 코드 ]
/**
* @param {number} n
* @param {number[][]} edges
* @return {number[]}
*/
const findSmallestSetOfVertices = function (n, edges) {
const connections = Array(n).fill(0);
const result = [];
edges.forEach(([from, to]) => connections[to] += 1);
connections.forEach((num, index) => num === 0 && result.push(index));
return result;
};